le 23 oct, 2021


2021 第3回　全統共通テスト模試　p-90 第1問　問4 「気体の溶解度」

<ポイント> 　
　
「気液平衡　飽和蒸気圧」　 液体があると，その上の空間には蒸気が・・・　

「ドルトンの分圧の法則」　 全圧からBの飽和蒸気圧を引くとAの分圧　

「気体の溶解度　ヘンリーの法則」　Aの分圧比が 溶解量の比

　　※　ポイントはいつもと同じです。　図に書き込みをしたので，まずそちらを参考に。

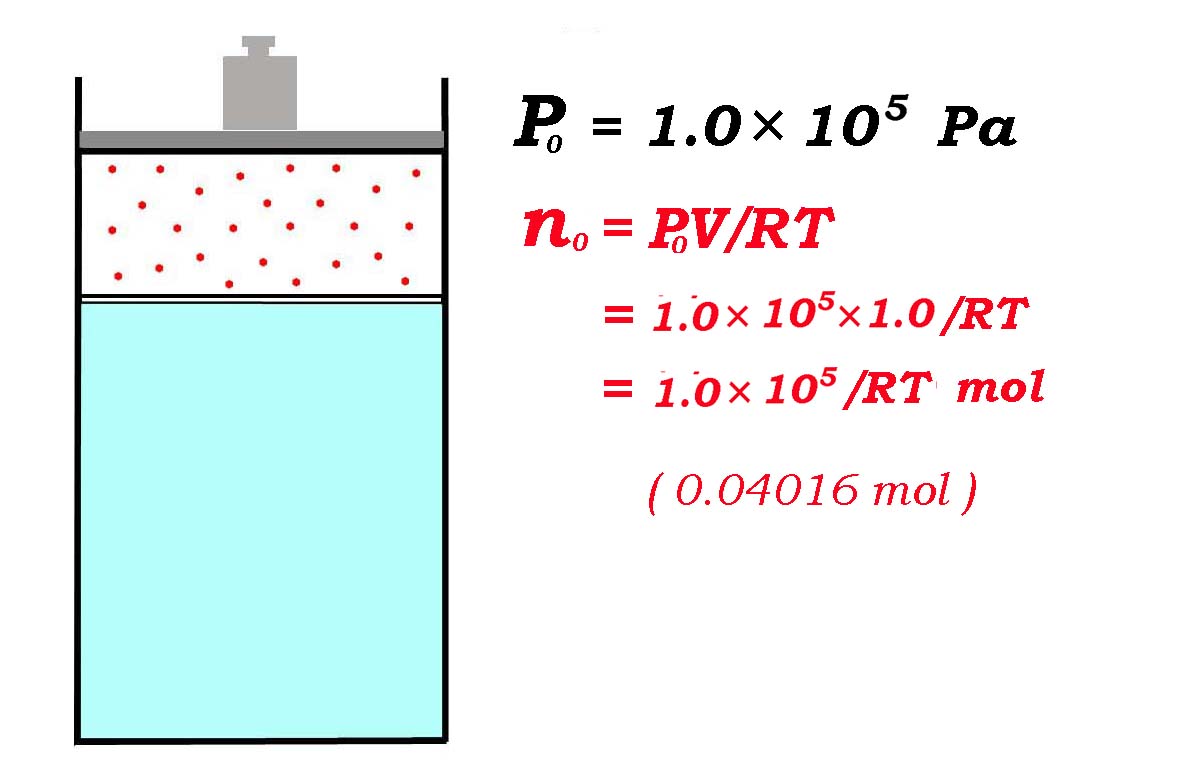
実験Ⅰ

　　はじめの状態　　２７℃　1.0×10⁵ Pa
　　
　　　　　　　　　　　　A 気体　1L 　/ 　仕切り板　/ 　B 水　3L

　　　仕切り板を取り除くと　Bは蒸発し，飽和蒸気圧となるので 　　　　　　　　　　　　　　　　　

　　　　　P_B = P_SAT = 2.0×10⁴ Pa

　　　　　全圧　P = 1.0×10⁵ Pa


　　　分圧の法則より　Aの分圧は，

　　　　　　P_A = P - P_B = 1.0×10⁵ － 2.0×10⁴ 　= 8.0 ×10⁴ Pa

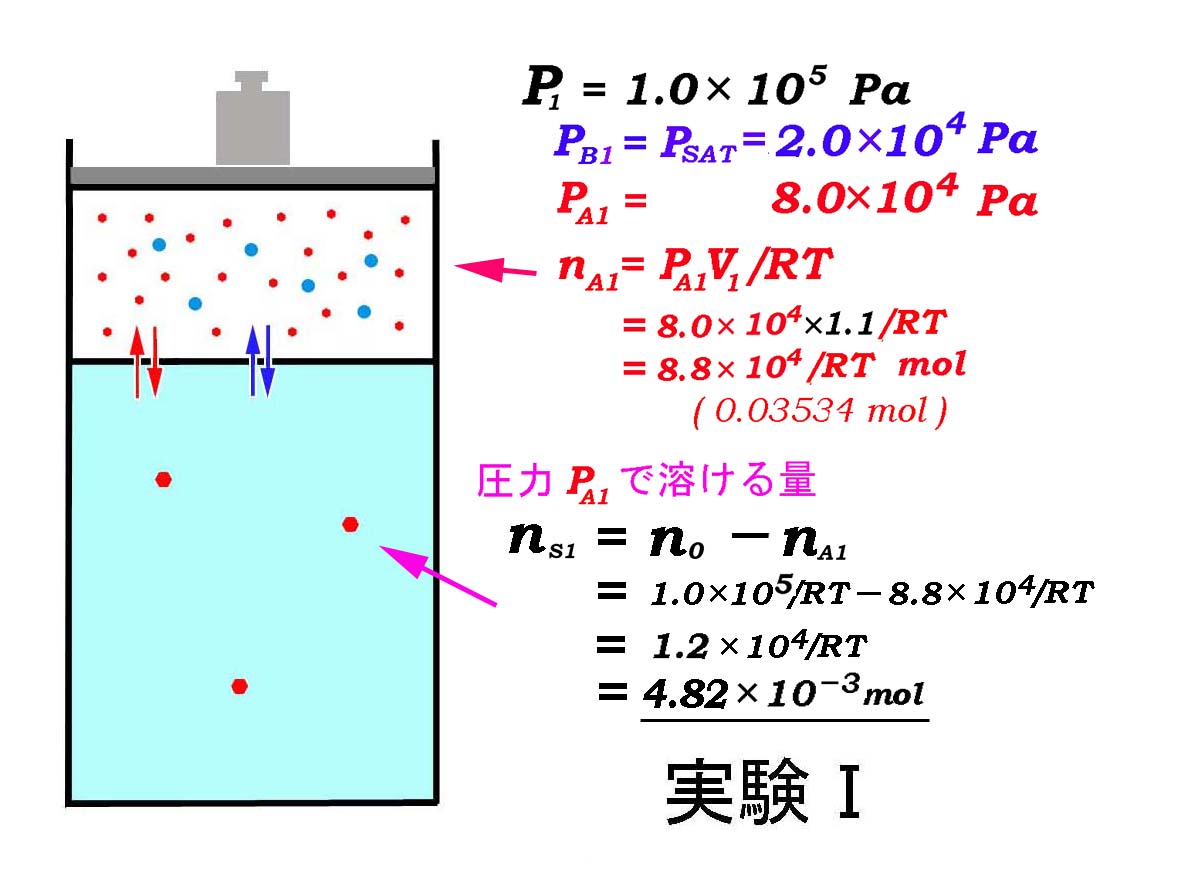
　　　気体Aの物質量は，

　　　　　　　n_A = P_AV/RT
　　　　　　　　　= 8.0×10⁴×1.1/RT
　　　　　　　　　= 8.8×10⁴/RT
　　　　　　　　　= 0.03534 mol

　　　水蒸気Bの物質量は，

　　　　　　　n_B = P_BV/RT
　　　　　　　　　= 2.0×10⁴×1.1/RT
　　　　　　　　　= 2.2×10⁴/RT
　　　　　　　　　= 0.0088 mol

実験Ⅱ

　　全圧を三倍にしたときも

　　　Bは気液平衡を保ち，飽和蒸気圧となるので　　　　　　　　　　　　　　　　　

　　　　　P_B = P_SAT = 2.0×10⁴ Pa
　
　　　全圧　P = 3.0×10⁵ Pa

　　　分圧の法則より　Aの分圧は，

　　　　　P_A = P - P_B = 3.0×10⁵ － 2.0×10⁴ 　= 2.8 ×10⁵ Pa

　　　※　Aの分圧は実験Ⅰのときの28/8 倍になったから

　　　　　ヘンリーの法則より溶解する物質量も28/8倍になる。




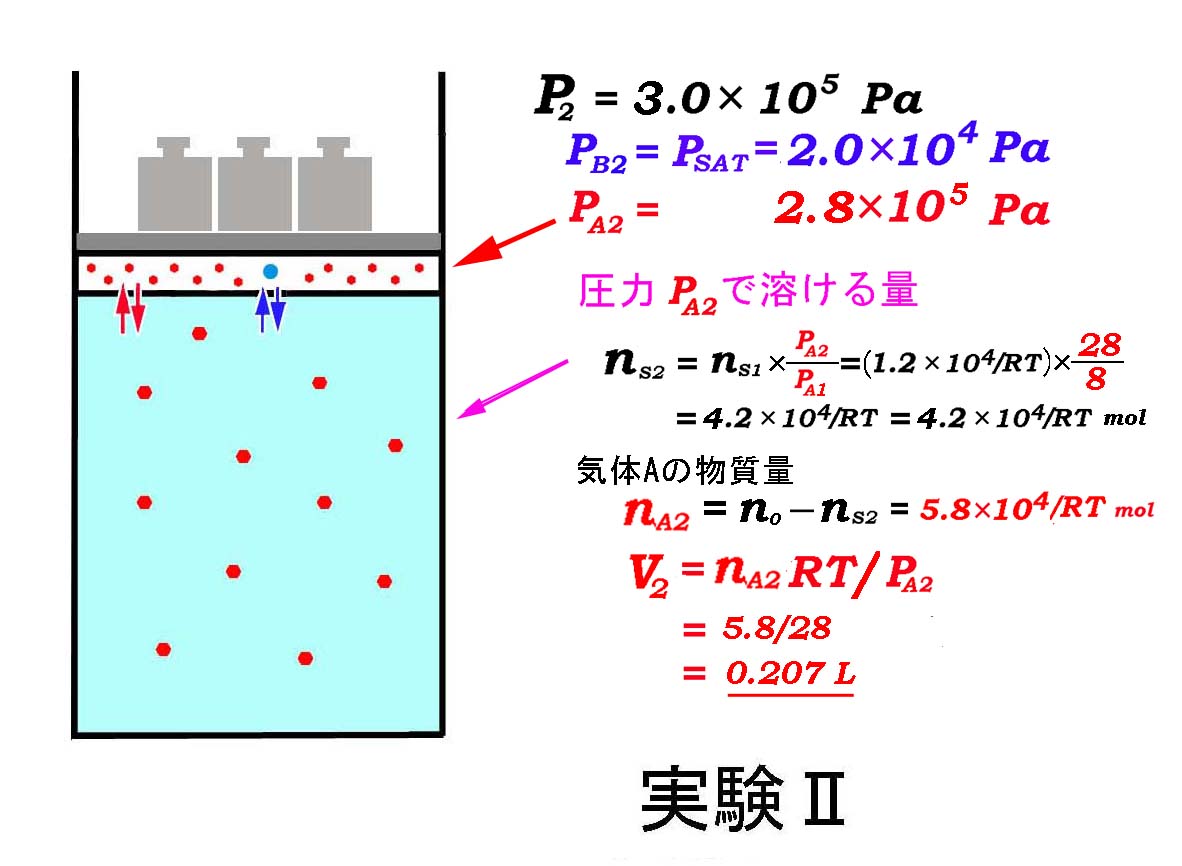
※　Aのはじめの全量から溶解している量を引くと気体部分のAの物質量

　　となる。(計算してみると，0.02329mol)

　　Aについて状態方程式から体積を求めるとよい。RTは消えてしまう。
　　

※　温度一定の実験条件なのでRTは共通となるから，いちいち8.3×10³×300で割ると
　　　　　
　　同じ割り算を繰り返すことになるので，RTは最後に代入しましょう。

※　この問題は苦手な分野が重なり，苦戦した人も多いのでは?　がんばりましょう。