東書p-95問4,5 図解

　　

※　まず問4を解いてみよう。



解法(1)　　代数的に

　　C(黒鉛)　　+ 　O₂　 = CO₂ + 394 kJ ･････①
　　C(ダイヤモンド) +　O₂ = CO₂ + 395 kJ ･････②

①－②　より
　　C(黒鉛) = C(ダイヤモンド) - 1 kJ

　　　　　　　　　　　　　　　　　　　　　　　　　答 －1 kJ/mol
　※　この演算方法を見つける。
　　　同じ側にあれば，＋。　反対側にあれば－とするだけで，
　　　式どうしを加減したり，移項したりはしないこと。



解法(2)　　図解して
　　
　　　　　　
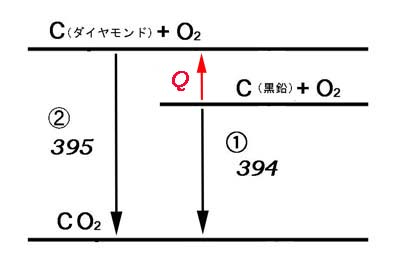
　　図より，　- Q + 394 = 395　　　
　　　　　　　　　　　　　　　　∴　Q = -1 　　答 －1 kJ/mol　


※ 　次に問5を解いてみよう。


解法(1)　　代数的に

　　C(黒鉛)　　+ 　O₂　 =　 CO₂+ 394 kJ ･････①
　　CO 　+　¹/₂ O₂ 　=　 CO₂ 　+ 283 kJ ･････②

①－2×②　より
　　
　　C(黒鉛)　+ 　CO₂　 = 　2 CO - 172 kJ

　　　　　　　　　　　　　　　　　　　　　　　答 －172 kJ/mol


解法(2)　　図解してみると，下図のようになり，
　　　　　　 この問については，(1)代数的解法の方が速い。
　　
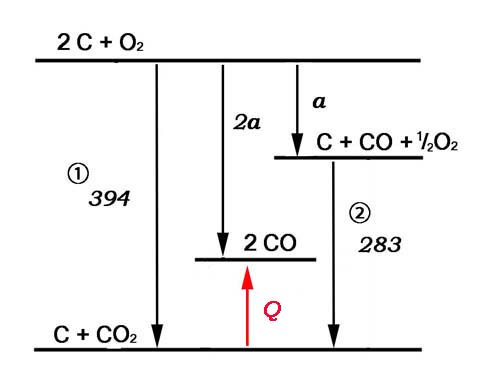
　　※　aは，COの生成熱である。

　　　　　　a + 283 = 394 　 　∴ a = 111
　　　　　　　
　　　　-Q + 2a = 394 　　 ∴Q = - 172

　　　　　　　　　　　　　　　　　　　　　　　　答 －172 kJ/mol


※　ヘスの法則の図解の手順

　　 1.問題に登場する熱化学方程式のうち，
　　　　原子数の最も多いものに注目。
　　　　　
　　　　※　ここでは，C (黒鉛) + CO₂ = 2 CO　の式。　　　　　

　　　2.含まれる元素を全て単体にして，
　　　　　エネルギーの最上部に書く。
　　　
　　　　※　C原子が2個，O原子が2個だから，単体は 2 C(黒鉛) + O₂

　　 3. 反応物(左辺)と生成物(右辺)にわけて書く。

　　　※　それぞれすこし左右に寄せて書くとわかりやすい。
　　　　　　C (黒鉛) + CO₂ と， 2 CO　　

　　4. ↓の変化は発熱。↑は吸熱。
　　　　　　　何熱かを考え，数値を入れる。

　　　　※　どのレベルでも各原子数が同じになるように。
　　　　　　　　　　　　　　　　　変化していない物質もそのまま書く。